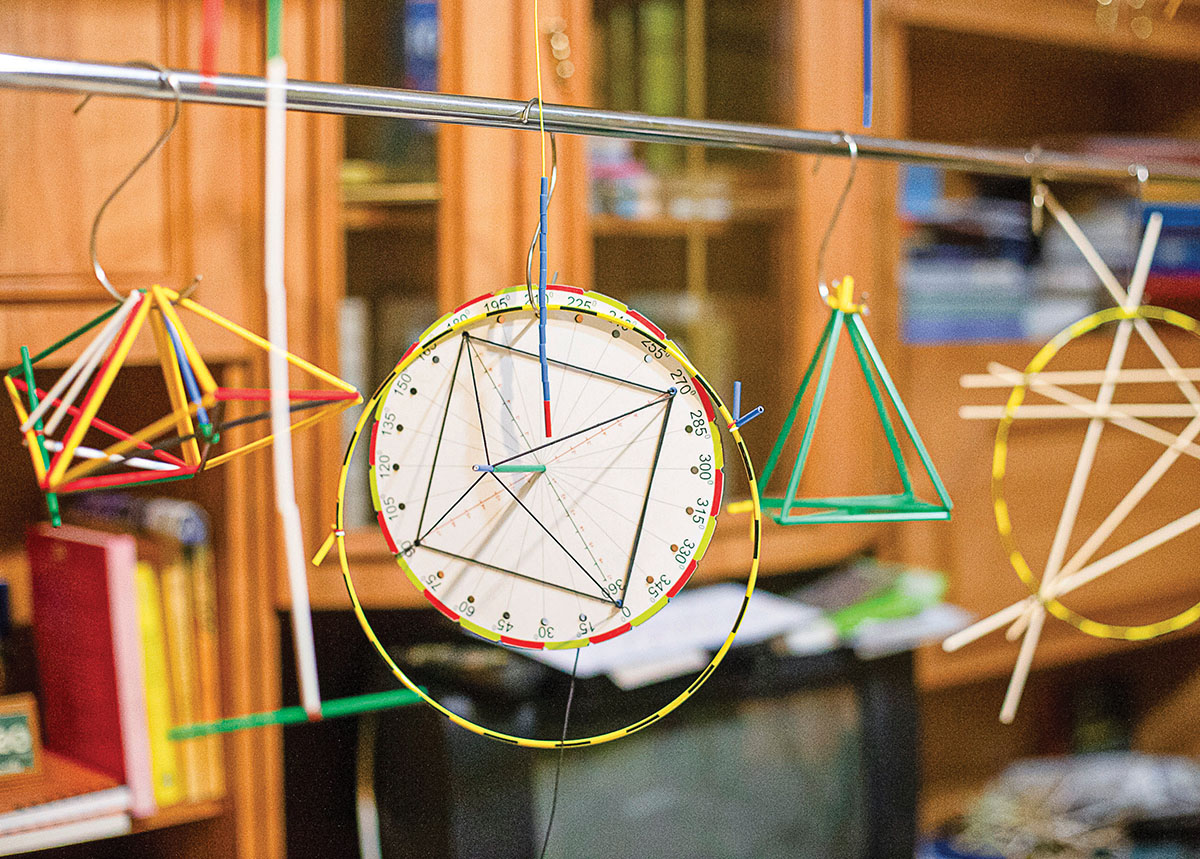– Hogy emlékszik vissza, évekkel ezelőtt is ilyen problematikus volt megtanítani és megértetni a diákokkal a matematika „nyelvét”?

– Napjainkra nagyon megcsappant a teljesítmény, ez a legnagyobb gond. Matematikából mindjárt gyengébbek az eredmények, mint románból, és ez főként a rossz oktatáspolitika miatt van. 1974‑ben kezdtem fizikát tanítani Tordán, azt követően kerültem több állomás után a székelyudvarhelyi Bethlen Gábor Általános Iskolába. Annak idején reáltudományokból, fizikából, kémiából, matematikából minden gyermek kísérleteket végzett, szaklaboratóriumok voltak, meg volt adva a lehetőség a tapasztalatszerzésre. Pályafutásom elején akkora volt a lelkesedés, hogy három szakkört kellett naponta tartanom: elméleti és kísérleti fizikát, feladatmegoldást, valamint matematikát. Olyan osztályom is volt, hogy mára harminckét diákból huszonöt egyetemi tanár lett különféle műszaki egyetemeken. Hogy mi történt? Korábban, a poroszos keretek között, az a tanár, aki szerette a munkáját, rengeteg befektetett energiával, kevés pénzért nagy sikereket és eredményeket tudott felmutatni, de aztán fordulat jött: a szabadságot a tanügyben felváltotta a szabadosság, a kontroll hiánya. Én emlékszem, ezerkétszáz lej volt a fizetésem, abból ötszázat vitt a lakbér és ötszázat az élelem, kétszáz lejből nagy nyaralásokat, puccos bevásárlásokat nem tervezett az ember, a figyelmét a tanításra fordította. Most megfizetik a tanárokat, de nincs sok elkötelezett tanár, ahogy diák sem. Mivel más a diák hozzáállása, máshogyan is kell tanítani. A TikTok‑nemzedékek idejét éljük, mikor gyorsan és hatékonyak kell összevont módszerekkel tanítani. A fizikát nem lehet elválasztani a matektől, sem az informatikától, mikor a kiterjesztett valóság egyre inkább átkerül a digitális térbe, ami ugyancsak a matematika nyelvén működik.

– Tapasztalataim szerint a számtantanuláshoz áldozatos, kitartó munka, de főként idő kell. Hogy lehet úgy gyorsan tanítani, hogy az a diákok fejében meg is maradjon?

– Meg kell nézni, hogy mi hiányzik a diák tudásából, és ezt differenciáltan kell felmérni egyénekre lebontva. Meg kell nézni azt is, hogy a diák mennyire elkötelezett a feladatok elvégzésére, érti vagy nem érti, hogyan lehet segíteni neki ebben, milyen készségeit kell megmozgatni, hogy könnyebben rögzítse a matematikai gondolkodást. Ami ma van a tanügyben, az nem megy. Beszéltem én a magyar és román oktatási miniszterekkel, előbbi azt mondta: két hete ismerem a munkáját, negyven éve dolgozunk, de odáig még nem jutottunk, mint maga. Ez két éve volt. Akkor megbeszéltük, hogy eljönnek ide és bemutatom a módszerem hatvan gyermekkel. Nem tették. Gyorsítva különben nem lehetetlen tanítani. Ha megnézik a nyolcadikosok tételsorát, hatvannégy dolog van, amit tudni kell, és ez tulajdonképpen négy év tudását ellenőrzi. Kicsit elbolondították a tanárokat és a szülőket a sok példatárral és munkafüzettel. Üzletet csináltak belőle. Közben a tételeket és a képleteket négy A4‑es oldalról meg lehet tanulni.

– Sok száz, pálcákból és gumiszalagokból összeállított mértani forma és test – ezek az ön módszerének az alapelemei. Kifejtené, hogy hogyan válik kis idő alatt eredményessé ez a tapasztaláson alapuló matektanulás?

– A módszer lényege, hogy enaktív, cselekvéses módon építse meg a diák azt az ábrát, térformát, ami a megoldandó feladat alanya, ezzel térben is szemlélve, könnyebben megértve az összefüggéseket. Ha vesszük például a kört, ki tudja megmondani kapásból, hogy hogyan kell kiszámítani a kerületét? Majdnem senki. A gond eleve ott kezdődik, hogy nem értettük meg a kör felosztásának és tagolásának rendszerét: gondolok itt a húrokra, sugarakra, de még az átmérőre is. Ha van olyan modell, amin kísérleti jelleggel lehet szögeket lemérni, irányokat, metszeteket megfigyelni, sokkal egyszerűbben megérti a diák, hiszen nem egy elméleti firka lesz róla a fejében, hanem az általa felfedezett és megépített rendszer. Így lehet mérni, megfigyelni, hogy miként változnak a szögek, milyen módosításokkal írhatók be egy körbe különféle síkidomok, és az általa felfedezett területet rendszerint jobban ismeri és jobban boldogul vele az ember, mintha csak a fejébe tömnék.

– Öröm az ürömben, hogy módszerével ingyen fejleszthetik számtantudásuk a diákok. Nem néznek emiatt Önre ferde szemmel azok a tanárok, akik pénzért korrepetálnak?

– Dehogynem. Sőt, vannak olyan pedagógusok, akik a szülőket is megpróbálják lebeszélni erről. De erre valahol számítottam. Az egésznek az a lényege, hogy bebizonyítsuk a világnak: ezt mind meg lehet csinálni ingyen, csak máshogy kell megközelíteni a dolgot. Ezzel a projekttel tulajdonképpen az 1–4., 5–8., 9–12.-es diákoknak biztosítunk fejlődési lehetőséget, úgy, hogy a próbavizsgákon írt eredményeik garantáltan növekedni fognak három jegyet egy tizenöt órás képzést követően. Ehhez csak annyi szükséges, hogy a diák figyeljen oda és teljesítse a kiadott feladatokat. Ezek a képzések ingyenesek, nem áll mögöttem senki, az egész vagyonom beleáldoztam ebbe a projektbe és szeretném, ha célt is érne, megmutatkozna a diákok fejlődésében. Mikor meghirdettük a képzést, a következő napra már hatvanan jelentkeztek, e‑mailen kellett jelezzék a próbavizsgákon elért eredményeiket, ugyanakkor egy általunk összeállított tesztet is meg kell oldaniuk, amivel felmérjük a tudásukat. Aki nem tudja megoldani, annak odaadjuk a kidolgozott eredményeket, hogy rögzüljön a megoldási módszer. Ez a teszt főként azért van, hogy a diákoknak tudásszintjükhöz mérten tudjunk személyre szabott feladatokat adni. Különben a képzések megvalósításában külső segítséget is kapok, Szakács Paál‑István az inkubátorház egyik termét is felajánlotta, neki köszönhetően már megvan a képzések helyszíne.

– Értesülésem szerint speciális oktatásra szoruló diákok felkészítésében is segít. Hogyan tudott erre felkészülni, és milyen kiegészítő módszereket alkalmaz?

– A kidolgozott módszert alkalmazva tanítottam már nemlátókat, süketnémákat, más, sérülésekkel vagy hiányosságokkal élő egyéneket és figyelemzavaros gyermekeket is. Külön kellett képeznem magam, sokat olvastam és szakemberekkel konzultáltam arról, hogy hogyan is kell ezekben az esetekben pedagógusként eredményesen helytállni. Együttműködünk Márkus Attila budapesti professzorral, aki a számtantanulás nehézségeit, pszichológiáját és akadályait térképezte fel kutatómunkája során, ez a kapcsolat rendkívül értékes volt számomra. Ha részleteibe menően tekintjük, tulajdonképpen az egész matematika tananyagot sikerült kidolgozni az 5–12. osztály számára Braille‑írásban, a nemzetközileg elismert jelrendszer szerint. Ez azt jelenti, hogy egy‑egy test vagy síkidom oldalainak színei más‑más vonalvastagsághoz vannak rendelve, melyek kidomborodnak a munkalap felületéről. Ezeket tapintva tudja megkülönböztetni a látássérült diák, hogy melyik a két sárga befogó, melyik a kék szögfelező egy adott ábrán, és a teljesítendő instrukciót is hasonlóképp tudja elolvasni legyen szó domború latin betűről, arab számról vagy vakírásról. Ha látássérülteket tanítok, mindig elfedem egy kalappal vagy egyéb kiegészítővel a szemem, hogy hozzájuk hasonló állapottal szembesüljek. Ez sokat segít abban, hogy azonosulni tudjak, hiszen ha átérzem a hiányosságait, hatékonyabban tudom segíteni.